人们面对比较复杂的问题，有时需要把研究的对象按照一定的标准进行分类，并逐类进行讨论，再把每一类的结论综合，使问题得到解决。

这种解决问题的思想方法就是分类讨论的思想方法。

分类讨论是我们在日常生活以及科学研究中经常使用的思想方法。

比如我们在权衡是否要给孩子报某个辅导班时，就会按照报与不报来进行分类，比较其优劣。

而在数学里，分类讨论的思想更是从小学贯穿到高中整个阶段。

甚至可以说，越是往上，分类讨论思想的应用越是广泛。

分类讨论的实质是把不确定的大问题按照某种标准，进行切分，转化为若干个确定的小问题，分而治之，各个击破，最后再进行综合归纳。

其分类规则和解决问题的步骤是——根据研究的需要，确定同一分类标准（往往是基于对概念的理解），恰当的对研究对象进行分类，分类后的所有子项之间既不能交叉，也不能从属，而且所有子项的外延之和必须与被分类的对象的外延相等，通俗的说就是要做到不重不漏，逐类逐级的进行讨论，综合、概括、归纳，得到最后的结论。

全面、有序，是分类讨论非常重要的两个标准。

正因为如此，分类讨论问题对于学生思维的全面性、逻辑性培养很有益。

那么分类思想在小学数学教材中都是如何体现的呢？又应该如何培养呢?

在小学人教版数学教材一年级上册的《认识图形（一）》中有这么一幅图：

此处就是分类思想的一个应用，按照长方体、正方体、圆柱、球体四个模型，要求学生对日常生活中的物体进行分类。

在低年级，分类思想的渗透都是以此形式进行的。

所以分类思想在孩子低龄阶段并不是必须有教材的辅助，在生活中就有很多分类的案例。

比如有一次我们带孩子出去玩，在高速上车辆来来往往，我们就让孩子讨论如何对车进行分类，比如品牌、颜色、车型等标准都可以。

一年级下册第三单元《分类与整理》更是直接将分类与统计作为该单元的主要教学内容。

在这里，课本要求学生忽略掉颜色，以形状为标准来进行分类划分。

其实也可以让学生以颜色为标准来进行划分。

最后会发现，无论是哪种划分方式，最后的结果一定是不重不漏的。

这里的分类与整理蕴含了分类讨论思想，同时也是对统计思想的渗透。

在第8单元《数学广角——搭配》中，分类思想更是作为一个主要的思想应用。

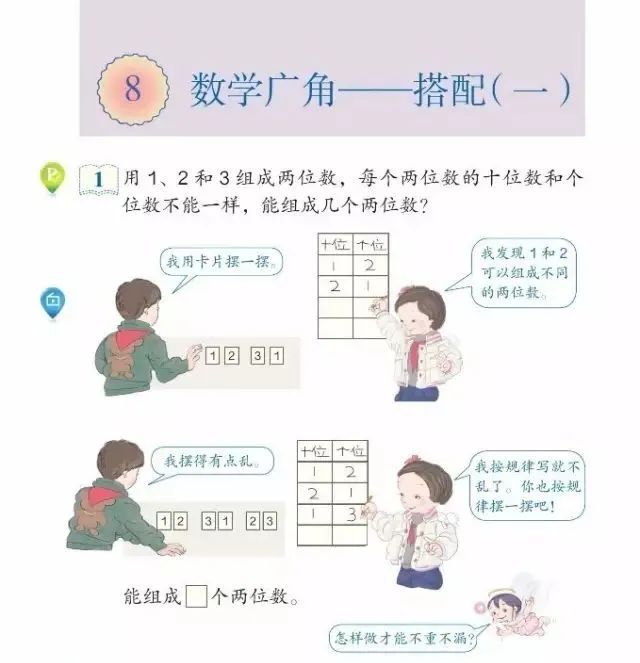
本单元的例1，实际上是一个排列问题，但在小学数学不学习排列组合的情况下，学生只能选择枚举法，而枚举法就以为着要有一定的分类标准——比如按照数字从小到大，按照标准进行，如此才能做到不重不漏。

在练习题中，有这么一道硬币的题目。

这道题首先要按照硬币的数量进行分类，之后再其内部进行组合。

相较于其他题目，在分类思想的考察上更有难度一些。

小学数学阶段的分类思想应用都与此类似，主要侧重于分类，强调的是分类的有序性和全面性，所以只能叫分类思想，不能叫分类讨论思想。

因为分类讨论有一个重要的部分，就是讨论，而讨论需要不确定性，这是小学数学大部分情况下不涉及的内容。

但是到了初中，甚至是七年级上册，分类讨论思想的应用就陡然增多。

中学数学属于典型的学的少，考的多、考的深，就比如七年级上册教材中，我扒了半天才在相反数那里找到这么一个涉及到分类讨论的点。

但是如果我们看看初中数学中的题目，就会发现分类讨论已经大行其道了。

比如这道题，是从点位置的不同情况入手进行分类讨论。

这道题，需要结合绝对值概念或者几何含义来进行分类讨论。

这道题，根据字母的正负情况来进行分类讨论。

这道题，需要结合绝对值概念和几何含义进行讨论，相较于前面几道题，在分类时需要确定分类标准，然后按照不同范围进行讨论。

这道题，需要结合一元一次方程的概念、解法步骤来进行分类讨论。

这道题涉及到枚举，也可以认为是分类讨论的一种，需要结合约束条件来进行。

这种题型需要结合点m的位置来进行讨论，进而找到思路，不是需要写出来的步骤，而是在解题时的思考过程，即使在高一也是常见的题型。

上题在分类讨论时则需要结合图形在运动中所处的不同位置。

这道题目则需要按照三角形相似的不同情况来分类讨论，建立方程。

（以上题目都来自于新思维）

由以上例子我们可以发现，需要初中分类讨论的试题基本类型包括：

考查数学概念的分类讨论

学生需要对于数学概念掌握扎实，遇到问题之后能够根据概念明确讨论标准。一般是围绕代数问题、方程不等式、函数来出题，比如绝对值的概念与几何含义、一元一次方程、一元二次方程的定义与解法。

考查图形的位置关系或形状

学生需要打开思维，不能拘泥于一种固定形式，需要按照一定的逻辑顺序来对不同几何特征进行讨论，比如直角顶点的位置，等腰三角形的腰的位置等，不漏是这种题型的基本要求。

考查图形的对应关系

比如三角形相似问题，对其中可能出现的有关点的可能对应情况加以分类讨论。

初中数学涉及分类讨论的常见问题

绝对值、应用题中的方案选择、解方程、等腰三角形腰、直角三角形顶点、相似三角形的对应点、动点问题、圆。

可以说，初中数学中分类讨论思想的应用已经很广泛，在各个知识点中都有所体现，而到了高中数学，在题型上会有所变化，平面几何的分类讨论问题被字母的取值情况或范围的讨论所取代。

这种题型在函数中比较多，主要是涉及到自变量的取值范围变化，往往会和图像结合比较紧密，会结合图像变换、函数性质、值域等内容考察；在方程、解析几何、数列、解三角形、向量中也会有所体现。

相较于初中数学，高中数学的分类讨论问题更复杂，更抽象一些。

比如上题，首先是划分层次，虽然是常数项含有字母，但我们并不是直接讨论字母的范围，而是根据题意，分类讨论判别式小于0或大于等于0的情况。

也就是说，分类讨论的对象不是字母，而是根据题意找到一个分类标准，比如这道题和根有关，那就应该考虑判别式，字母是包含在对判别式的分类中的。

比如这道题目，就涉及到对-a和-2a+1两个值大小的讨论，这是基于解一元二次不等式的步骤，必须要根据两者的大小关系才能明确其解集。

像这道题目，其分类讨论思路首先是考虑到函数图像的形态，进而讨论a的取值，但此处的a其实对应的是函数图像与x轴右侧交点的位置，仍然是有其背景的。

这道题的讨论情况比较多，如何做到不重不漏是一个难点，还是要基于对图像的认识。

很明显，我们发现分类讨论是自然发生的，并不是刻意为之，做题做到这里，面对解一元二次不等式，因为对不等式解法的掌握扎实，明确在此处必须要进行大小讨论才能往下做，不确定，那就必须进行讨论。

这就是所谓的分类讨论必定是基于基础概念、基础方法。

之所以大部分高中数学阶段的分类讨论题大都因概念而引发，是因为有些概念本身就包含多种情况，比如指、对数底数大小与单调性、不等式性质中涉及到乘除的一些性质、直线的斜率与倾斜角范围的关系等；有些概念本身有约束，比如二次函数、方程、不等式的二次项系数不为0、等比数列前n项和公式需要考虑公比是否为0等。

初中阶段的考察亦是如此。

出题人在命题时，为了提高题目难度，加大对学生概念掌握的考察力度，以及思维的逻辑性、缜密性、全面性考察，必然会在这些易忽略的地方设置分类讨论的点。

所谓没有无缘无故的爱，也没有无缘无故的分类讨论，很多孩子对分类讨论不够好，其根本原因还是基础不够扎实。

要掌握好分类讨论问题，一方面是概念搞清楚，搞扎实；

二是从一开始学习这种题型时就做好训练，分类标准要清晰，要有层次感，要着重注意不重不漏；

三是在解题时能够抓住主要矛盾，也就是确定分类讨论的标准。

适当的刷题是必须的，因为只有通过刷题才能提高敏感度和洞察力，知道在哪里讨论，如何讨论，才能熟悉出题老师的套路。

你可能还想读